Abstract

本算法用于实现井字棋游戏电脑先手情况下的智能落子

Introduction

关于井字棋的模块的搭建，分为棋盘的初始化、棋盘的展示、电脑落子、玩家落子、判断输/赢/平局/继续游戏这5个模块。

其中，我们着重介绍一下电脑落子的具体算法。本算法可以使得玩家永远赢不了棋局。（输/平局）

本算法的核心思想为 暴力枚举 和 迫使玩家进行指定位置的落子
注：

  1. 本棋盘为3*3的大小
  2. 电脑先手
  3. 以下用形如(2,1)的形式表示落子的坐标
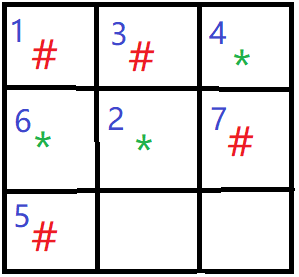
  4. 用“**#”表示电脑的棋子，用“***”表示玩家的棋子
  5. 代码部分使用C语言进行实现

    Algorithm

    Step1

    电脑的第一步永远落于(1,1)
    在这里插入图片描述

Step2

接下来，玩家落子一共有8个点可供选择，根据对称性，我们可以将其分分成5组。它们分别是：

  1. (1,2)或(2.1)
  2. (1,3)或(3,1)
  3. (2,3)或(3,2)
  4. (2,2)
  5. (3,3)

以下对于每一类情况进行分组讨论，每组以其中一种情况进行举例
蓝色的数字表示落子的顺序

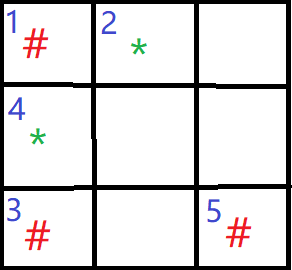
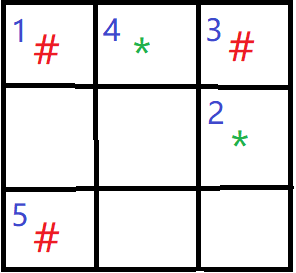
A.(1,2)

在这里插入图片描述
在这里插入图片描述

上图表示玩家第一手落于(1,2)的情况。此时，显然玩家必输。
同理，玩家落子于(2,1)，显然必输。

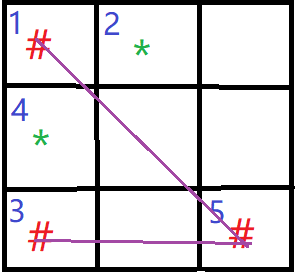
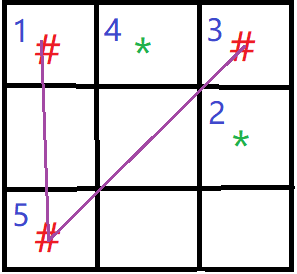
B. (1,3)

在这里插入图片描述
在这里插入图片描述

上图表示玩家第一手落于(1,3)的情况。此时，显然玩家必输。
同理，玩家落子于(3,1)，显然必输。

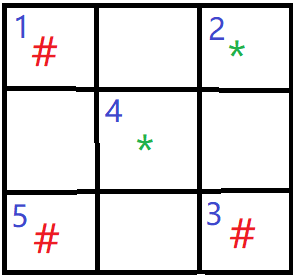
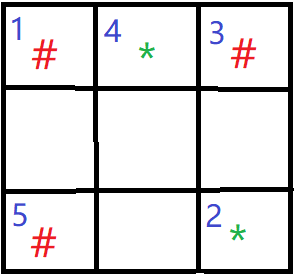
C.(2,3)

在这里插入图片描述在这里插入图片描述

上图表示玩家第一手落于(2,3)的情况。此时，显然玩家必输。
同理，玩家落子于(3,2)，显然必输。

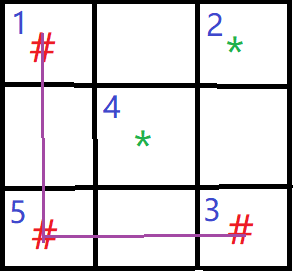
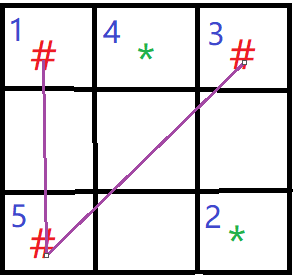
D.(3,3)

在这里插入图片描述
在这里插入图片描述

上图表示玩家第一手落于(3,3)的情况。此时，显然玩家必输。

E.(2,2)

在这里插入图片描述
上图表示玩家第一手落于(2,2)的情况。此时，显然最终双方会握手言和。

Step3

以下展示电脑落子的代码

首先需定义棋盘大小

1
2
#define ROW 3
#define COL 3

首先创建一个3*3的二维数组

1
char board[3][3]={0};

并将二维数组中每一个元素使用初始化模块初始化为’ ‘ ，也就是空格，此处省略

我们另需封装一个CountNum函数用来统计棋盘中的9个格子已经有几个格子上落了子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int CountNum(char board[ROW][COL], int row, int col)
{
	int count = 0;
	int i = 0;
	int j = 0;
	for (i = 0; i < row; i++)
	{
		for (j = 0; j < col; j++)
		{
			if (board[i][j] != ' ')
				count++;
		}
	}
	return count;
}

以下代码为具体的电脑落子智能算法，其中参数board表示用来表示棋盘的二维数组的地址，row为ROW（3），col为COL（3）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
void ComputerMove(char board[ROW][COL], int row, int col)
{
	int x = 0;
	int y = 0;
	if (CountNum(board, ROW, COL) == 0)
	{
		board[0][0] = '#';
	}
	if (CountNum(board, ROW, COL) == 2)
	{

		//5 types , 8 situations

		// 1
		if (board[0][1] == '*')
		{
			board[2][0] = '#';
		}
		// 2
		if (board[1][0] == '*')
		{
			board[0][2] = '#';
		}
		// 3 
		if (board[0][2] == '*')
		{
			board[2][2] = '#';
		}
		// 4
		if (board[2][0] == '*')
		{
			board[2][2] = '#';
		}
		// 5
		if (board[2][1] == '*')
		{
			board[2][0] = '#';
		}
		// 6
		if (board[1][2] == '*')
		{
			board[0][2] = '#';
		}
		// 7
		if (board[1][1] == '*')
		{
			board[0][1] = '#';
		}
		// 8
		if (board[2][2] == '*')
		{
			board[0][2] = '#';
		}
	}
	if (CountNum(board, ROW, COL) == 4)
	{
		// 1@1
		if (board[0][1] == '*' && board[2][0] == '#')
		{
			if (board[1][0] == '*')
			{
				board[2][2] = '#';
			}
			else
			{
				board[1][0] = '#';
			}
		}
		// 2@1
		if (board[1][0] == '*' && board[0][2] == '#')
		{
			if (board[0][1] == '*')
			{
				board[2][2] = '#';
			}
			else
			{
				board[0][1] = '#';
			}
		}
		// 3@1
		if (board[0][2] == '*' && board[2][2] == '#')
		{
			if (board[1][1] == '*')
			{
				board[2][0] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 4@1
		if (board[2][0] == '*' && board[2][2] == '#')
		{
			if (board[1][1] == '*')
			{
				board[0][2] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 5@1
		if (board[2][1] == '*' && board[2][0] == '#')
		{
			if (board[1][0] == '*')
			{
				board[0][2] = '#';
			}
			else
			{
				board[1][0] = '#';
			}
		}
		// 6@1
		if (board[1][2] == '*' && board[0][2] == '#')
		{
			if (board[0][1] == '*')
			{
				board[2][0] = '#';
			}
			else
			{
				board[0][1] = '#';
			}
		}
		// 7@1
		if (board[1][1] == '*' && board[0][1] == '#')
		{
			if (board[0][2] == '*')
			{
				board[2][0] = '#';
			}
			else
			{
				board[0][2] = '#';
			}
		}
		// 8@1
		if (board[2][2] == '*' && board[0][2] == '#')
		{
			if (board[0][1] == '*')
			{
				board[2][0] = '#';
			}
			else
			{
				board[0][1] = '#';
			}
		}
	}
	if (CountNum(board, ROW, COL) == 6)
	{
		// 1@1@1
		if (board[0][0] == '#' && board[2][0] == '#' && board[2][2] == '#' && board[0][1] == '*' && board[1][0] == '*')
		{
			if (board[1][1] == ' ')
			{
				board[1][1] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 2@1@1
		if (board[0][0] == '#' && board[0][2] == '#' && board[2][2] == '#' && board[0][1] == '*' && board[1][0] == '*')
		{
			if (board[1][1] == ' ')
			{
				board[1][1] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 3@1@1
		if (board[0][0] == '#' && board[2][0] == '#' && board[2][2] == '#' && board[0][2] == '*' && board[1][1] == '*')
		{
			if (board[1][0] == ' ')
			{
				board[1][0] = '#';
			}
			else
			{
				board[2][1] = '#';
			}
		}
		// 4@1@1
		if (board[0][0] == '#' && board[0][2] == '#' && board[2][2] == '#' && board[2][0] == '*' && board[1][1] == '*')
		{
			if (board[0][1] == ' ')
			{
				board[0][1] = '#';
			}
			else
			{
				board[1][2] = '#';
			}
		}
		// 5@1@1
		if (board[0][0] == '#' && board[2][0] == '#' && board[0][2] == '#' && board[1][0] == '*' && board[2][1] == '*')
		{
			if (board[0][1] == ' ')
			{
				board[0][1] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 6@1@1
		if (board[0][0] == '#' && board[0][2] == '#' && board[2][0] == '#' && board[0][1] == '*' && board[1][2] == '*')
		{
			if (board[1][0] == ' ')
			{
				board[1][0] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
		// 7@1@1
		if (board[0][0] == '#' && board[0][1] == '#' && board[2][0] == '#' && board[1][1] == '*' && board[0][2] == '*')
		{
			if (board[1][0] == '*')
			{
				board[1][2] = '#';
			}
			else
			{
				board[1][0] = '#';
			}
		}
		// 8@1@1
		if (board[0][0] == '#' && board[0][2] == '#' && board[2][0] == '#' && board[0][1] == '*' && board[2][2] == '*')
		{
			if (board[1][0] == ' ')
			{
				board[1][0] = '#';
			}
			else
			{
				board[1][1] = '#';
			}
		}
	}
	if (CountNum(board, ROW, COL) == 8)
	{
		//7@1@1@1
		if (board[0][0] == '#' && board[0][1] == '#' && board[1][2] == '#' && board[2][0] == '#' && board[0][2] == '*' && board[1][0] == '*' && board[1][1] == '*')
		{
			if (board[2][1] == '*')
			{
				board[2][2] = '#';
			}
			else
			{
				board[2][1] = '#';
			}
		}
	}
}

Acknowledgment

谢谢我自己能在大一下期中考前抽出半天来研究这样一个看似挺无聊的问题

谢谢小伙伴们能够看完这篇文章

附上GitHub完整代码

如果想要深入了解AI对弈，可以去看看极大极小算法（Minimax）

本人目前水平有限，如有错误，望指正

2021.4.24 姑苏阴雨绵绵